| Appendix IV. Approximate distribution of herbivore production, foraging preference model. |
| To derive equations describing equilibrium values of the logistic plant growth model incorporating foraging preference parameter a, I started with text equation (24), the foraging preference model: |
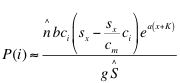 (IV-A) (IV-A)
converted to the logarithmic “x” axis; x = ln(ci) and xm = ln(cm)
 (IV-B) (IV-B)
collecting terms and rearranging:
 (IV-C) (IV-C)
 (IV-D) (IV-D)
integrating along the x-axis and rearranging (IV-D) yields:
 (IV-E) (IV-E)
 (IV-F) (IV-F)
 (IV-Fa) (IV-Fa)
|
To evaluate herbivore production by plants with values of x [x = ln(ci)] between Xm and –K (K = xmin = ln(minimum value of ci)) is done by first evaluating for x= xm then subtracting the value for x = xm - K:
|
 [x = xm] (IV-G) [x = xm] (IV-G)
 [x = xm - Z] (IV-H) [x = xm - Z] (IV-H)
 (IV-J) (IV-J)
subtracting IV-J from IV-G:
 (IV-K) (IV-K)
 (IV-L) (IV-L)
Collecting terms gives the number of herbivores pruduced by plants within Z log units of xm on the axis of plant suitability:
 (IV-M) (IV-M)
|
| To calculate the proportion of the total herbivore production represented by (IV-M) above, we need to know the total herbivore production. This is done by evaluating equation IV-Fa at x = -K and subtracting from IV-G above. |
 (IV-N) (IV-N)
 [K>6; exp(-K) approaches 0] (IV-O) [K>6; exp(-K) approaches 0] (IV-O)
The proportion of the total herbivore production will then be:
 (IV-P) (IV-P)
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
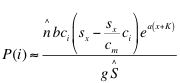 (IV-A)
(IV-A) (IV-B)
(IV-B) (IV-C)
(IV-C) (IV-D)
(IV-D) (IV-E)
(IV-E) (IV-F)
(IV-F) (IV-Fa)
(IV-Fa) [x = xm] (IV-G)
[x = xm] (IV-G) [x = xm - Z] (IV-H)
[x = xm - Z] (IV-H) (IV-J)
(IV-J) (IV-K)
(IV-K) (IV-L)
(IV-L) (IV-M)
(IV-M) (IV-N)
(IV-N) [K>6; exp(-K) approaches 0] (IV-O)
[K>6; exp(-K) approaches 0] (IV-O) (IV-P)
(IV-P)